Cómo calcular la vida media
 Share
Share
En esta sección, aprenderemos sobre la vida media y derivaremos la fórmula para calcular la vida media. En la radiactividad, media vida es el tiempo que tarda la mitad de los núcleos radiactivos en una muestra de un isótopo radioactivo en descomposición. El número de núcleos radiactivos en una muestra decae exponencialmente con el tiempo. Para calcular la vida media, por lo tanto, se utilizan las matemáticas de la descomposición exponencial. La vida media es un concepto extremadamente importante para aplicaciones de radioactividad. Los radioisótopos introducidos en los órganos en la radioterapia, por ejemplo, no deben permanecer en el cuerpo de un paciente durante demasiado tiempo. Por otro lado, los isótopos utilizados para fechar artefactos históricos deben tener una vida media larga, de modo que haya suficientes de ellos hasta el día de hoy para determinar la edad de los objetos..
Diferencia entre la naturaleza aleatoria y espontánea de la desintegración radiactiva
La desintegración radiactiva se clasifica como ambos aleatorio y espontáneo.
- La desintegración radioactiva es aleatoria porque no podemos determinar cuándo un núcleo dado se desintegrará, o determinar cuánto tiempo tomaría antes de que un núcleo dado se desintegrara. En consecuencia, cada núcleo radiactivo en una muestra tiene la misma probabilidad de descomposición en un momento dado.
- La desintegración radiactiva es espontánea. Porque no se ve afectado por condiciones externas..
Que es Half Life
El número de núcleos radiactivos en una muestra está disminuyendo, porque una vez que el núcleo se descompone a través de la desintegración alfa, beta y gamma, no pueden volver a sufrir el mismo proceso de desintegración. El número de núcleos radiactivos en la muestra disminuye exponencialmente.
los actividad, o la tasa de descomposición,Es la tasa de cambio del número de núcleos radiactivos. Esto es dado por,

El signo negativo significa que el número de núcleos radiactivos en una muestra es decreciente a través del tiempo. $ latex \ lambda & s = 1 $ se llama el constante de descomposición. Da la probabilidad de que un núcleo dado se desintegre por unidad de tiempo. La constante de desintegración tiene un valor específico para cualquier proceso de desintegración nuclear dado. Cuanto mayor sea el  , cuanto mayor es la probabilidad de descomposición y el número de núcleos radiactivos en la muestra disminuye más rápidamente.
, cuanto mayor es la probabilidad de descomposición y el número de núcleos radiactivos en la muestra disminuye más rápidamente.
Si el número de núcleos radiactivos en una muestra a la vez  es
es  , entonces el número de núcleos radiactivos
, entonces el número de núcleos radiactivos  en la muestra despues de un tiempo
en la muestra despues de un tiempo  es dado por:
es dado por:

El número de núcleos radiactivos en la muestra disminuye. exponencialmente. Media vida ( ) Es la cantidad de tiempo que se tarda en reducir a la mitad el número de núcleos radiactivos en el tiempo. Si dibujamos una gráfica de cómo varía el número de núcleos radiactivos en la muestra a lo largo del tiempo, obtenemos la siguiente gráfica:
) Es la cantidad de tiempo que se tarda en reducir a la mitad el número de núcleos radiactivos en el tiempo. Si dibujamos una gráfica de cómo varía el número de núcleos radiactivos en la muestra a lo largo del tiempo, obtenemos la siguiente gráfica:

Cómo calcular la vida media - Curva de desintegración radiactiva
Cómo calcular la actividad
La actividad de la muestra es proporcional al número de núcleos radiactivos presentes. Entonces, podemos hacer una declaración equivalente,

dónde  Es la actividad de la muestra en el momento.
Es la actividad de la muestra en el momento.  , con
, con  la actividad cuando
la actividad cuando  .
.
Si se dibuja una gráfica de la actividad en función del tiempo, producirá una gráfica con la misma forma (es decir, la actividad también decae exponencialmente).
La actividad se mide con la unidad SI. becquerel (bq). Una actividad de 1 Bq corresponde a una tasa de 1 decaimiento por segundo. los curie (Ci) Es otra unidad utilizada para medir la actividad. 1 Ci = 3.7 × 1010 Bq.
Formula Half Life
Ahora derivaremos una fórmula para obtener la vida media de la constante de descomposición. Empezamos con,

Después de un tiempo  , El número de mitades de núcleos radiactivos. Asi que,
, El número de mitades de núcleos radiactivos. Asi que,  , o
, o

Tomando el logaritmo natural de ambos lados, obtenemos:

y entonces,

Cómo calcular la vida media
Ejemplo 1
El indio-112 tiene una vida media de 14,4 minutos. Una muestra contiene 1,32 × 10.24 átomos de indio-112.
a) Encuentra la constante de descomposición
b) Averigüe cuántos átomos de Indio-112 quedarían en la muestra después de 1 hora.
a) Desde  ,
,

b) utilizando  ,
,  átomos.
átomos.
Ejemplo 2
Durante un tratamiento para el cáncer de tiroides, un paciente recibe una muestra de yodo-131 para ingerir, que tiene una actividad de 1,10 MBq. La vida media de Iodine 131 es de 8.02 días.. Encuentre la actividad del yodo-131 en el cuerpo del paciente después de 5 días de ingestión.
Usamos  . Primero trabajamos
. Primero trabajamos  :
:

Entonces,
 Mbq.
Mbq.
Nota:
- Calculamos directamente la constante de descomposición por día y mantuvimos la vida media también en días. Así que los días cancelados cuando calculamos
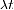 y no había necesidad de convertir tiempos en segundos (eso también habría funcionado, pero habría implicado un poco más de cálculo)
y no había necesidad de convertir tiempos en segundos (eso también habría funcionado, pero habría implicado un poco más de cálculo) - En realidad, la actividad sería más pequeña. Esto se debe a que también hay una vida media biológica asociada con la actividad. Esta es la velocidad a la que el paciente excreta núcleos radioactivos de su cuerpo..
Ejemplo 3
Calcule la vida media de un isótopo radioactivo cuya actividad se reduce en un 4% a lo largo de 1000 años.
4% = 0.04. Ahora tenemos
 . Tomando ln de ambos lados,
. Tomando ln de ambos lados,
 por año.
por año.
 216 años.
216 años.
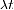 y no había necesidad de convertir tiempos en segundos (eso también habría funcionado, pero habría implicado un poco más de cálculo)
y no había necesidad de convertir tiempos en segundos (eso también habría funcionado, pero habría implicado un poco más de cálculo)