Diferencia entre igual y equivalente
 Share
Share
Diferencia Principal - Igual vs. Equivalente
Igual y equivalente Son términos que se usan frecuentemente en las matemáticas. los diferencia principal entre igual y equivalente es que el termino igual se refiere a cosas que son similares en todos los aspectos, mientras que el término equivalente se refiere a cosas que son similares en un aspecto particular. Tenga en cuenta que en el teoría de conjuntos, las palabras "igual" y "equivalente" tienen significados específicos, como veremos a continuación.
¿Qué significa igual?
En general, dos cosas son iguales si son similares en todos los aspectos..
En el caso de la teoría de conjuntos, dos conjuntos son iguales si ambos contienen los mismos elementos. los orden en el que se enumeran en un conjunto no importa. Por ejemplo, supongamos
 y
y
 entonces,
entonces,
el conjunto  es igual al conjunto
es igual al conjunto  .
.
¿Qué significa equivalente?
Se puede decir que dos cosas son equivalentes si son similares en una condición particular. Por lo tanto, si dos entidades son equivalente en gran parte depende en la condición que usamos para describir su equivalencia. Por ejemplo, los números 2 y 7 son equivalentes en el sentido de que ambos son números primos. Sin embargo, si la condición que nos interesa es averiguar si los números son pares, en este sentido, 2 y 7 son no equivalente. Usamos los simbolos  o
o  para indicar que
para indicar que  y
y  son equivalentes.
son equivalentes.
Una vez que se ha definido un criterio, las cosas que son equivalentes satisfacen la relaciones de equivalencia:
- Reflexividad:
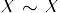
- Simetría: Si
 , entonces
, entonces 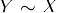
- Transitividad: Si
 y
y 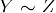 , entonces
, entonces 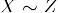
En la teoría de conjuntos, dos conjuntos son equivalente Si tienen el mismo número de elementos. Los elementos en sí mismos no necesitan ser los mismos, tampoco, solamente El número de elementos debe ser el mismo. Por ejemplo, supongamos
 y
y
 entonces,
entonces,
los conjuntos  y
y  son equivalentes.
son equivalentes.

Símbolos para expresar igualdad y equivalencia.
Diferencia entre igual y equivalente
Significado general
Cuando dos cosas son igual, Son similares en todos los aspectos..
Cuando las cosas estan equivalente, Son similares en un aspecto particular..
En la teoría de conjuntos
Cuando dos sets son igual, contienen los mismos elementos.
Cuando dos sets son equivalente, contienen lo mismo número de elementos.
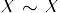
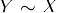
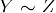 , entonces
, entonces