Diferencia entre T-test y ANOVA
 Share
Share
 Hay una línea delgada de demarcación en medio de la prueba t y ANOVA, es decir, cuando se comparan las medias poblacionales de solo dos grupos, prueba t se utiliza, pero cuando se comparan medios de más de dos grupos, ANOVA se prefiere.
Hay una línea delgada de demarcación en medio de la prueba t y ANOVA, es decir, cuando se comparan las medias poblacionales de solo dos grupos, prueba t se utiliza, pero cuando se comparan medios de más de dos grupos, ANOVA se prefiere.
La prueba T y el análisis de varianza, abreviados como ANOVA, son dos técnicas estadísticas paramétricas utilizadas para probar la hipótesis. Como estos se basan en el supuesto común de que la población a partir de la cual se toma la muestra se debe distribuir normalmente, la homogeneidad de la varianza, el muestreo aleatorio de los datos, la independencia de las observaciones, la medición de la variable dependiente en la relación o el nivel de intervalo, las personas a menudo interpretan mal dos.
Aquí, se presenta un artículo para que comprenda la diferencia significativa entre la prueba t y ANOVA, eche un vistazo.
Contenido: T-test Vs ANOVA
Gráfica comparativa
| Bases para la comparación | Prueba de t | ANOVA |
|---|---|---|
| Sentido | La prueba T es una prueba de hipótesis que se utiliza para comparar las medias de dos poblaciones. | ANOVA es una técnica estadística que se utiliza para comparar las medias de más de dos poblaciones.. |
| Estadística de prueba | (x ̄-µ) / (s / √n) | Variación entre muestras / Variación dentro de la muestra |
Definición de T-Test
La prueba t se describe como la prueba estadística que examina si las medias poblacionales de dos muestras difieren mucho entre sí, utilizando la distribución t que se usa cuando no se conoce la desviación estándar y el tamaño de la muestra es pequeño. Es una herramienta para analizar si las dos muestras se extraen de la misma población..
La prueba se basa en el estadístico t, que asume que la variable se distribuye normalmente (distribución simétrica en forma de campana) y se conoce la media y se calcula la varianza de la población a partir de la muestra.
En t-test la hipótesis nula toma la forma de H0: µ (x) = µ (y) contra hipótesis alternativa H1: µ (x) ≠ µ (y), donde µ (x) y µ (y) representan las medias poblacionales. El grado de libertad de la prueba t es n1 + norte2 - 2
Definición de ANOVA
El Análisis de Varianza (ANOVA) es un método estadístico, comúnmente utilizado en todas aquellas situaciones en las que se realiza una comparación entre más de dos medias de población, como el rendimiento del cultivo a partir de múltiples variedades de semillas. Es una herramienta vital de análisis para el investigador que le permite realizar pruebas simultáneamente. Cuando usamos ANOVA, se supone que la muestra se extrae de la población normalmente distribuida y la varianza de la población es igual.
En ANOVA, la cantidad total de variación en un conjunto de datos se divide en dos tipos, es decir, la cantidad asignada al azar y la cantidad asignada a causas particulares. Su principio básico es probar las variaciones entre los medios de la población mediante la evaluación de la cantidad de variación dentro de los ítems del grupo, proporcional a la cantidad de variación entre los grupos. Dentro de la muestra, la varianza se debe a la alteración aleatoria sin explicación, mientras que un tratamiento diferente puede causar una varianza de la muestra.
Con el uso de esta técnica, probamos, hipótesis nula (H0) donde todas las medias poblacionales son iguales, o hipótesis alternativa (H1) donde al menos una media poblacional es diferente.
Diferencias clave entre T-test y ANOVA
Las diferencias significativas entre T-test y ANOVA se discuten en detalle en los siguientes puntos:
- Una prueba de hipótesis que se usa para comparar las medias de dos poblaciones se llama prueba t. Una técnica estadística que se utiliza para comparar las medias de más de dos poblaciones se conoce como Análisis de varianza o ANOVA..
- La estadística de prueba para la prueba de T es:
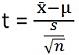 La estadística de prueba para ANOVA es:
La estadística de prueba para ANOVA es: 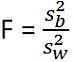
Conclusión
Después de revisar los puntos anteriores, se puede decir que la prueba t es un tipo especial de ANOVA que se puede usar cuando tenemos solo dos poblaciones para comparar sus medias. Aunque las posibilidades de errores pueden aumentar si se usa la prueba t cuando tenemos que comparar más de dos medios de las poblaciones al mismo tiempo, es por eso que se usa ANOVA
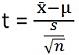 La estadística de prueba para ANOVA es:
La estadística de prueba para ANOVA es: