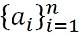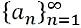Diferencia entre secuencia y serie
Share
En matemáticas y estadística, la línea que delimita la secuencia y la serie es delgada y borrosa, debido a que muchos piensan que estos términos son lo mismo. Sin embargo, la noción de secuencia difiere de la serie en el sentido de que secuencia se refiere a una disposición en el orden particular en el que los términos relacionados se suceden, es decir, tiene una primera unidad identificada, una segunda unidad, una tercera unidad, etc..
Cuando una secuencia sigue una regla particular, se llama como progresión. No es exactamente lo mismo que serie que se define como la suma de los elementos de una secuencia. Lea el artículo para conocer la diferencia significativa entre secuencia y serie..
Contenido: Secuencia Vs Series
Gráfica comparativa
| Bases para la comparación | Secuencia | Serie |
|---|---|---|
| Sentido | La secuencia se describe como el conjunto de números u objetos que siguen un patrón determinado. | Serie se refiere a la suma de los elementos de la secuencia.. |
| Orden | Importante | A veces importante |
| Ejemplo | 1, 3, 5, 7, 9, 11… n… | 1 + 3 + 5 + 9 + 11… n… |
Definición de secuencia
En matemáticas, un conjunto ordenado de objetos o números, como un1, una2, una3, una4, una5, una6… unanorte… . se dice que están en una secuencia, si, según cierta regla, tiene un valor definido. Los miembros de la secuencia se llaman término o elemento que es igual a cualquier valor del número natural. Cada término en una secuencia está relacionado con el término anterior y el siguiente. En general, las secuencias tienen reglas o patrones ocultos que le ayudan a descubrir el valor del siguiente término..
El término n es la función del entero n (positivo), considerado como el término general de la secuencia. Una secuencia puede ser finita o infinita..
- Secuencia finita: Una secuencia finita es aquella que se detiene al final de la lista de números a1, una2, una3, una4, una5, una6… unanorte, está representado por:
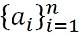
- Secuencia infinita: Una secuencia infinita se refiere a una secuencia que es interminable, una1, una2, una3, una4, una5, una6… unanorte… .., está representado por:
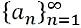
Definición de serie
La adición de los términos de una secuencia (unnorte), es conocido como serie. Al igual que la secuencia, la serie también puede ser finita o infinita, donde una serie finita es aquella que tiene un número finito de términos escritos como1 + una2 + una3 + una4 + una5 + una6 + … unanorte. A diferencia de las series infinitas, donde el número de elementos no es finito o que no tiene fin, se escribe como1 + una2 + una3 + una4 + una5 + una6 + … unanorte +... .
Si un1 + una2 + una3 + una4 + una5 + una6 + … unanorte = Snorte, entonces Snorte Se considera como la suma a n elementos de la serie. La suma de los términos a menudo se representa mediante la letra griega sigma (). Por lo tanto,
Diferencias clave entre secuencia y serie
La diferencia entre secuencia y serie se puede dibujar claramente por los siguientes motivos:
- La secuencia se define como la colección de números u objetos que siguen un patrón definido. Cuando los elementos de la secuencia se suman, se conocen como series..
- El orden importa en una secuencia, ya que hay una cierta regla que prescribe el patrón de la secuencia. Por lo tanto, 1, 2, 3tres es diferente de 3, 1, 2. Por otro lado, en un orden de aparición en serie puede o no importar, como en el caso de series absolutamente convergentes, el orden no importa. Entonces, 1 + 2 + 3 es igual que 3 + 1 + 2, solo su secuencia es diferente.
Conclusión
La progresión aritmética (A.P.) y la progresión geométrica (G.P.) también son secuencias, no series. La progresión aritmética es una secuencia en la que hay una diferencia común entre los términos consecutivos, como 2, 4, 6, 8 y así sucesivamente. Por el contrario, en una progresión geométrica, cada elemento de la secuencia es el múltiplo común del término anterior, como 3, 9, 27, 81 y así sucesivamente. De manera similar, la secuencia de Fibonacci es también una de las secuencias infinitas populares, en la que cada término se obtiene sumando los dos términos anteriores 1, 1, 3, 5, 8, 13, 21, etc..
