Cómo encontrar las asíntotas de una hipérbola
 Share
Share
Hipérbola
La hipérbola es una sección cónica. El término hipérbola se refiere a las dos curvas desconectadas que se muestran en la figura.
Si los ejes principales coinciden con los ejes cartesianos, la ecuación general de la hipérbola tiene la siguiente forma:

Estas hipérbolas son simétricas alrededor del eje y y se conocen como hipérbola del eje y. La hipérbola simétrica alrededor del eje x (o hipérbola del eje x) viene dada por la ecuación,
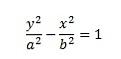 Cómo encontrar las asíntotas de una hipérbola.
Cómo encontrar las asíntotas de una hipérbola.
Para encontrar las asíntotas de una hipérbola, use una manipulación simple de la ecuación de la parábola.
yo. Primero lleva la ecuación de la parábola a la forma dada arriba
Si la parábola se da como mx2+Nueva York2=l, definiendo
una= √ (l/metro) y segundo= √ (-l/norte) dónde l<0
(Este paso no es necesario si la ecuación se da en el estándar de.

ii. Luego, reemplaza el lado derecho de la ecuación con cero.

iii. Factorizar la ecuación y tomar soluciones.

Por lo tanto, las soluciones son ,

Las ecuaciones de las asíntotas son.

Las ecuaciones de las asíntotas para la hipérbola del eje x también se pueden obtener mediante el mismo procedimiento.
Encuentre las asíntotas de una hipérbola - Ejemplo 1
Considera la hipérbola dada por la ecuación x2/ 4-y2/ 9 = 1. Encuentra las ecuaciones de las asíntotas..

Reescribe la ecuación y sigue el procedimiento anterior..
X2/ 4-y2/ 9 = x2/ 22 -y2/ 32 = 1
Al reemplazar el lado derecho con cero, la ecuación se convierte en x2/ 22 -y2/ 32 = 0.
Factorizando y tomando solución de la ecuación.,
(x / 2-y / 3) (x / 2 + y / 3) = 0
Las ecuaciones de las asíntotas son.,
3x-2y = 0 y 3x + 2y = 0
Encuentre las asíntotas de una hipérbola - Ejemplo 2
- La ecuación de una parábola se da como -4x² + y² = 4

Esta hipérbola es una hipérbola del eje x..
Reorganizar los términos de la hipérbola en el estándar a partir de da
-4x2+ y2= 4 => y2/ 22 -X2/ 12 = 1
Factorizar la ecuación proporciona lo siguiente
(y / 2-x) (y / 2 + x) = 0
Por lo tanto, las soluciones son y-2x = 0 y y + 2x = 0.
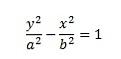 Cómo encontrar las asíntotas de una hipérbola.
Cómo encontrar las asíntotas de una hipérbola. 